Cargando...
Recursos educativos
-
Nivel educativo
-
Competencias
-
Tipología
-
Idioma
-
Tipo de medio
-
Tipo de actividad
-
Destinatarios
-
Tipo de audiencia
-
Creador
Lo más buscado
- Cine infantil
- Centenas, decenas y unidades
- Ejercicios resueltos
- Instrumentos musicales
- Actividades de repaso
- Competencias básicas
- Descargar ejercicios de ortografía
- Repaso de historia
- Biosfera
- juegos ortografía
- Aprender a contar
- Nombre de ríos
- Siglo XVIII
- Capitales de América
- Ilustraciones del ciclo del agua
-

Producto mixto: propiedades
estudiia Organización
- 3108 visitas
Deducimos algunas propiedades del producto mixto de tres vectores libres en el espacio.
-

Halla. Módulo de un vector 2
EduBook Organización
- 1 lo usan
- 2221 visitas
Indica cuáles de entre los vectores siguientes poseen el mismo módulo que el vector = (–3, 4):
-
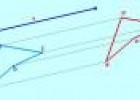
Movimientos en el plano: Traslación
INTEF Organización
- 1 lo usan
- 6559 visitas
Explicación sobre los vectores y sus movimientos de traslación sobre el plano.
-

Halla. Módulo de un vector 1
EduBook Organización
- 1889 visitas
Calcula el módulo de los siguientes vectores: = (5, –12) || = = (12, 16) || = = (–1, √3) || =
-

Módulo de un vector 1
EduBook Organización
- 1806 visitas
Halla el módulo de los siguientes vectores: = (–3, –4) → = (12, –5) → = (1, –√3) →
-

Indica. Módulo de un vector
EduBook Organización
- 1633 visitas
Indica cuáles de entre los vectores siguientes poseen el mismo módulo que el vector = (–3, 4):
-

Halla. Módulo de un vector 1
EduBook Organización
- 1410 visitas
Calcula el módulo de los siguientes vectores: = (5, –12) || = = (12, 16) || = = (–1, √3) || =
-

Halla. Módulo de un vector
EduBook Organización
- 1366 visitas
Halla el módulo de los siguientes vectores: = (–3, –4) → = (12, –5) → = (1, –√3) →
-

Calcula. Componentes de un vector
EduBook Organización
- 2164 visitas
Recuerda responder según las siguientes indicaciones: Dados los vectores = (3, –5), = (0, 4) y = (–1, –2), calcula algebraicamente las componentes de estos vectores: + = – = 2 + = + – = + =…
-

Ángulo de dos rectas
estudiia Organización
- 20406 visitas
Obtenemos la fórmula del coseno del ángulo que forman dos rectas (secantes o cruzadas) a partir de sus vectores directores.
Te estamos redirigiendo a la ficha del libro...













